Bài toán hóc búa từ 3500 năm trước cuối cùng đã có lời giải

Nội dung bài toán được phát biểu đơn giản như sau : cho trước một tập hợp gồm các số nguyên dương,àitoánhócbúatừnămtrướccuốicùngđãcólờigiảem gái khắc việt là ai hỏi từ tập hợp này có thể chọn ra các phần tử có tổng nghịch đảo bằng 1 được hay không?

Bài toán 3500 tuổi này có nguồn gốc từ thời Ai Cập cổ đại và trong một bài báo của mình, nhà toán học Thomas Bloom đã giải quyết trọn vẹn bài toán này. Một phiên bản của bài toán này cũng được hai nhà toán học Erdős và Graham đặt ra và trao thưởng 500 USD cho ai giải được nó.

Bài toán đó được đưa phát biểu như sau “Nếu tập A là tập con của tập N và A có mật độ dương, thì tồn tại một tập con hữu hạn S của A mà tổng nghịch đảo các phần tử của nó bằng 1”. (Một ví dụ về tập con của N có mật độ dương là A = { 3,5,7,9,11,...}, có thể hiểu nôm na là khi ta lấy một lượng đủ lớn các số tự nhiên liên tiếp thì xác suất để tồn tại một số thuộc vào A là khác 0).

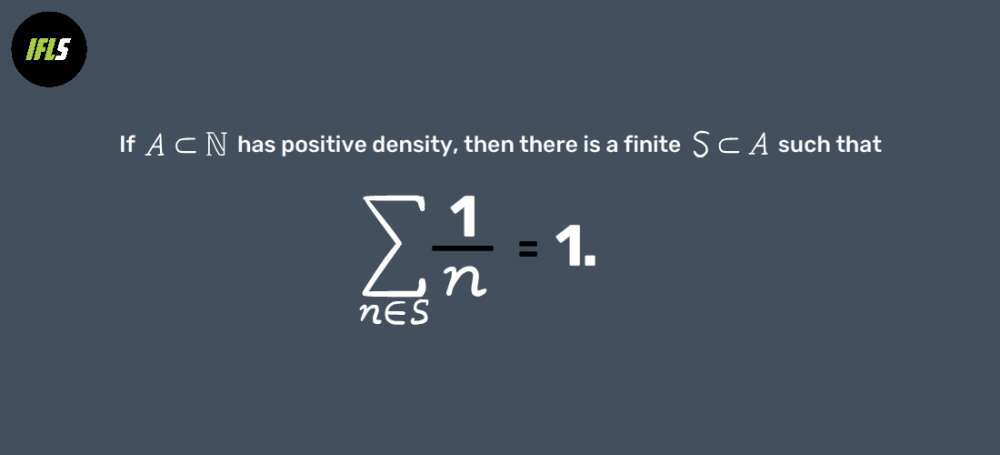Andrew Granville, một nhà toán học đến từ Đại học Montreal, nói trong Tạp chí Quanta : “Tôi chỉ nghĩ đây là một câu hỏi bất khả thi mà không ai có thể giải được. Tôi không thấy bất kỳ công cụ rõ ràng nào có thể giải quyết nó". Tuy nhiên, Bloom tình cờ đã tìm ra đáp án nhờ vào một bài báo có từ 20 năm trước trong Biên niên sử Toán học năm 2003 mà tác giả của nó là nhà toán học Ernie Croot.

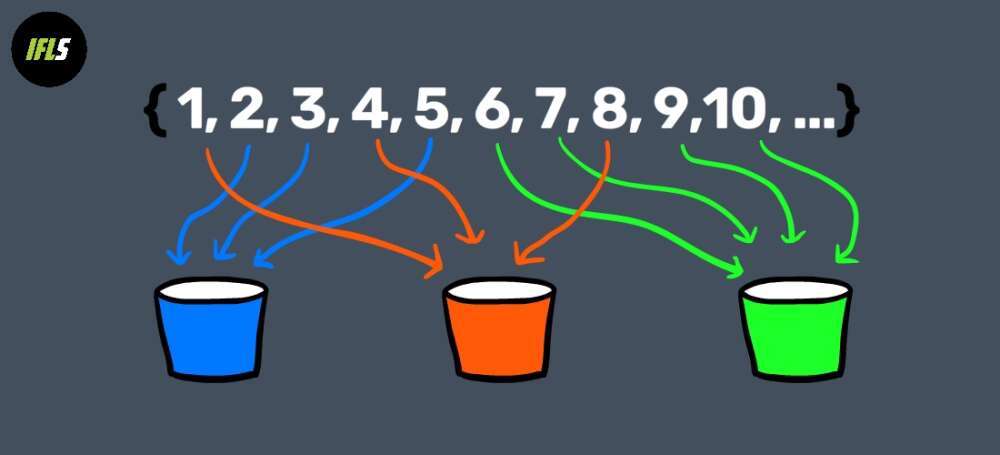
Những gì Croot đã giải được gọi là “phiên bản tô màu” của bài toán Erdős – Graham. Nó được gọi như vậy bởi vì nó liên quan đến các tập con “tô màu” - về cơ bản, có thể coi nó giống như việc phân chia tập A bằng cách bỏ các phần tử của A vào một số hữu hạn các hộp có màu khác nhau.

Nhà toán học Giorgis Petridis từ Đại học Georgia nói với Quanta: “Ý tưởng mả Croot đưa ra rất tuyệt vời. Tuy nhiên, nó đòi hỏi sự sáng tạo, khéo léo với các kỹ thuật tính toán cao” Petridis chia sẻ.

Ngoài ra, có một sự khác biệt rằng trong bài toán tô màu là, toàn bộ tập hợp A đã được chia thành các hộp. Bạn không biết chính xác nó được phân chia như thế nào, nhưng điều đó không thực sự quan trọng - tất cả những gì bạn cần chỉ ra là có một hộp chứa các con số đủ đẹp để tính tổng. Croot đã xây dựng bằng chứng để chỉ ra rằng sẽ có ít nhất một hộp có đủ những con số đẹp thỏa mãn định lý.

Nhưng phép chứng minh của Croot không giải được phiên bản trù mật của bài toán đã nói ở trên. Bloom đã vận dụng tốt những ý tưởng của Croot để giải quyết trọn vẹn bài toán. "Tôi nghĩ, phương pháp của Croot [thực sự] mạnh hơn so với tưởng tượng. Vì vậy, tôi đã dành ra vài tuần và tìm ra đáp án cho bài toán này" - Ông nói.

Bloom cho rằng Croot đã chứng minh được một trường hợp đặc biệt của bài toán này. Tất cả những gì Bloom phải làm là chỉ ra rằng kết quả sẽ giống nhau khi chứng minh các trường hợp còn lại và phiên bản trù mật của bài toán sẽ được giải quyết hoàn toàn.

Các phương pháp mà Bloom sử dụng thực sự là “một phiên bản nâng cấp” của những ý tưởng do Croot đề ra. Ý tưởng của Bloom là thay vì tìm ra các số có tổng nghịch đảo bằng 1 thì lại tìm ra các nhóm số có tổng nhỏ hơn, sau đó cộng lại bằng 1. “Ví dụ nếu ta tìm được ba nhóm mà tổng nghịch đảo các số của mỗi nhóm bằng ⅓ theo cách khác nhau, thì chỉ cần cộng chúng với nhau thì ta có kết quả là 1” - Bloom nói với tờ Quanta.

Với chứng minh của mình, Bloom đã giải quyết được một câu hỏi có nguồn gốc từ thời Ai Cập cổ đại. Tuy nhiên, không dừng ở đây, Bloom đặt ra một câu hỏi mới và tiếp tục đi tìm chứng minh: đối với tập A ⊂ N nào thì không thể tìm được tập con của A có tổng nghịch đảo các phần tử bằng 1?

Doãn Hùng (Theo IFL Science)

Tù nhân giải được bài toán cổ từng khiến nhà toán học 'đau đầu'

Một tù nhân tại Mỹ đã tự học toán cao cấp cơ bản. Nhờ đó, anh ta đã giải được một bài toán phức tạp. Không những thế, còn truyền niềm đam mê toán học của mình cho các bạn tù.